记录:C++ 生成正态分布随机数速度有点慢
只有代码和结果。没有分析。
1. 环境
首先,我的环境如下。我是在以下环境中运行后边的程序的:
# uname -a:
Linux (---) 5.15.0-72-generic #79~20.04.1-Ubuntu SMP Thu Apr 20 22:12:07 UTC 2023 x86_64 x86_64 x86_64 GNU/Linux
# g++ --version:
g++ (Ubuntu 9.4.0-1ubuntu1~20.04.1) 9.4.0
Copyright (C) 2019 Free Software Foundation, Inc.
This is free software; see the source for copying conditions. There is NO
warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
# clang++ --version:
clang version 10.0.0-4ubuntu1
Target: x86_64-pc-linux-gnu
Thread model: posix
InstalledDir: /usr/bin
# go version:
go version go1.20.3 linux/amd64
2. 代码和输出
现在,我用 C++ 编写能够生成正态分布的随机数的程序。代码如下:
// benchmark_normal_distribution.cpp
#include <random>
#include <cstdio>
#include <cstdlib>
#include <chrono>
struct StandardNormalDistribution {
std::default_random_engine generator;
std::normal_distribution<double> distribution;
// Methods:
StandardNormalDistribution();
double generate();
};
StandardNormalDistribution::StandardNormalDistribution() {
this->generator = std::default_random_engine();
this->distribution = std::normal_distribution<double>();
}
double StandardNormalDistribution::generate() {
return this->distribution(this->generator);
}
void generate_standard_normally_distributed_numbers(int N) {
auto started_at = std::chrono::steady_clock::now();
StandardNormalDistribution normal;
double *numbers = (double *)malloc(N * sizeof(double));
for (int i = 0; i < N; i++) {
numbers[i] = normal.generate();
}
free(numbers);
auto finished_at = std::chrono::steady_clock::now();
std::chrono::duration<double> time_used = finished_at - started_at;
printf("%d, %f\n", N, time_used.count());
}
int main() {
const int N = 10000000; // 10 millions
printf("N, time_used_cpp\n");
for (int i = 0; i < 10; i++) {
generate_standard_normally_distributed_numbers(i * N);
}
}
在开头描述的测试环境中,使用 g++ 编译上面的程序,运行,结果如下:
N, time_used_cpp
0, 0.000005
10000000, 1.800984
20000000, 3.606356
30000000, 5.403939
40000000, 7.224273
50000000, 9.022062
60000000, 10.839035
70000000, 12.657207
80000000, 14.472248
90000000, 16.364334
意思就是说,生成一千万(10_000_000)个随机数,需要 1.800984 秒;生成两千万个的话就要用 3.606356 秒。以此类推。
接下来,用 clang++ 编译运行,结果如下:
N, time_used_cpp
0, 0.000004
10000000, 4.733402
20000000, 9.393835
30000000, 14.110681
40000000, 18.779981
50000000, 23.465807
60000000, 28.189041
70000000, 32.888470
80000000, 37.610277
90000000, 42.306022
意思就是说,用 clang++ 的话,生成一千万(10_000_000)个随机数,需要 4.733402 秒;生成两千万个的话就要用 9.393835 秒。以此类推。
然后,用 Golang 编写功能一样的程序,代码如下:
// benchmark_normal_distribution.go
package main
import(
"math/rand"
"time"
"fmt"
)
func GenerateStandardNormallyDistributedNumbers(N int) {
startedAt := time.Now()
var (
numbers = make([]float64, N)
normal = rand.New(rand.NewSource(99))
)
for i := 0; i < N; i++ {
numbers[i] = normal.NormFloat64()
}
finishedAt := time.Now()
timeUsed := finishedAt.Sub(startedAt)
fmt.Println(N, ", ", timeUsed.Seconds())
}
func main() {
const N int = 10_000_000
fmt.Println("N, time_used_golang")
for i := 0; i < 10; i++ {
GenerateStandardNormallyDistributedNumbers(i * N)
}
}
编译并运行这个 Golang 程序,输出如下:
N, time_used_golang
0 , 4.7842e-05
10000000 , 0.256289357
20000000 , 0.495714572
30000000 , 0.727294915
40000000 , 0.971995647
50000000 , 1.161648942
60000000 , 1.47045757
70000000 , 1.747184227
80000000 , 1.9542733669999999
90000000 , 2.262972592
3. 整理
把输出的结果合并在一起:
N, time_used_cpp_gnu, time_used_cpp_clang, time_used_golang_120
0, 0.0000050, 0.000004, 4.7842e-05
10000000, 1.8009840, 4.733402, 0.256289357
20000000, 3.6063560, 9.393835, 0.495714572
30000000, 5.4039390, 14.110681, 0.727294915
40000000, 7.2242730, 18.779981, 0.971995647
50000000, 9.0220620, 23.465807, 1.161648942
60000000, 10.839035, 28.189041, 1.470457570
70000000, 12.657207, 32.888470, 1.747184227
80000000, 14.472248, 37.610277, 1.954273367
90000000, 16.364334, 42.306022, 2.262972592
(上面的 CSV 格式文本,可以直接复制粘贴到 Excel 里面,然后就能画折线图了)
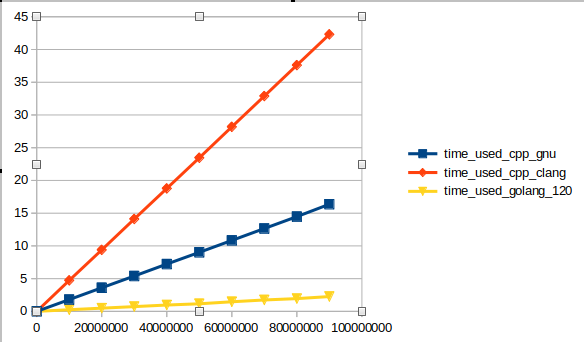
(横轴是生成的独立同分布的随机数数量,纵轴是用了多少秒)
4. 一些注记
- C++ 里面的
default_random_engine是 implementation-dependent 的,也就是说,不同的 stl 会有不同的实现。- 但是 llvm 的和 gnu 的也差太多了。
- 听说 C++ 用的是 Box-Muller Transform 但只是听说,并没有自己查证过
- Golang 用的是一种修改过的 rejection sampling。那个方法又怪又快。
- Golang 所用的这个方法 比较值得一记
- 可能是我的 g++ 和 clang++ 版本太老了。
- 做这个测试的起因是因为我想用蒙特卡洛方法估算下面的这个东西(这到底是什么东西,我并不知道,我也不想知道):
\begin{equation*} e^{-rT} \cdot \mathbb{E} \left[ { \left(\frac{1}{T} \int_{t=0}^{t=T} S_t dt - K\right)^{+} } \right] \end{equation*}
其中 $S_t := S_0 \exp \{ (r - \sigma^2 / 2) t + \sigma B_t \}$ 对所有 $t \ge 0$,$S_0, \sigma, r, K, T$ 为已知常数,$\{B_t\}_{t \ge 0}$ 为标准布朗运动过程。符号 $\mathbb{E}$ 代表期望值。符号 $(\cdot)^{+}$ 代表 $\max \{0, \cdot \}$。
只是单纯的报告而已。正文完。
更新
- (2023-06-02): LLVM 的 libc++ 用的是 Masaglia polar method。